1170 yılında İtalya’nın Pisa şehrinde doğan Leonardo Fibonacci’nin çocukluğu, babasının gümrük memurluğu nedeniyle Kuzey Afrika ‘da geçmiştir. Fibonacci, o dönemde matematik biliminde Avrupa’dan çok daha ileride olan İslam dünyasında matematik eğitimi aldı. 1200 yılında Pisa’ya geri döndü. Pisa’da, batı matematiğinin Arap rakamları ve ondalıklı sayıları keşfetmesini sağlayan ‘ Liber Abaci’ yani ‘Hesap Kitabı’ adlı ünlü eserini
yazdı. Ancak, Fibonacci’nin yenilikleri sadece bu kültür alışverişinden ibaret değildi. Fibonacci, doğanın düzeninin matematiksel yapısını ortaya çıkarmak amacıyla yaptığı
çalışmalarla, ölümünden sonraki dönemlerde bilim ve sanat dünyasında devrim sayılabilecek gelişmelere ön ayak olmuştur.
Fibonacci serisi sayıları:0, 1,1,2,3,5,8,13,21,34,55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, … vb. şeklinde devam eder. Her sayı kendisinden önce gelen iki sayının toplamıdır. Bu durumda genel olarak n'inci Fibonacci sayısı F(n) şu şekilde ifade edilir:
Fibonacci sayılarının ilginç özellikleri vardır. Mesela n sayısı büyüdükçe iki ardışık Fibonacci sayısının oranı Altın oran'a yani 1.618... e yakınsar.
Altın oran, doğada bir bütünün parçaları arasında gözlemlenen, yüzyıllarca sanat ve mimaride uygulanmış, uyum açısından en yetkin boyutları verdiği sanılan geometrik ve sayısal bir oran bağıntısıdır. Doğada en belirgin örneklerine insan vücudunda, deniz kabuklularında ve ağaç dallarında rastlanır. Platon'a göre kozmik fiziğin anahtarı bu orandır. Altın oranı bir dikdörtgenin boyunun enine olan "en estetik" oranı olarak tanımlayanlar da vardır.Altın oran sadece dikdörtgen ve doğru için değil neredeyse tüm geometrik cisimler ve yapılar için kullanılır.
Eski Mısırlılar ve Yunanlılar tarafından keşfedilmiş, mimaride ve sanatta kullanılmıştır. Göze çok hoş gelen bir orandır.
Altın Oran; CB / AC = AB / CB = 1.618; bu oranın değeri her ölçü için 1.618 dir.
Bir doğru parçasının (AB) Altın Oran'a uygun biçimde iki parçaya bölünmesi gerektiğinde, bu doğru öyle bir noktadan (C) bölünmelidir ki; küçük parçanın (AC) büyük parçaya (CB) oranı, büyük parçanın (CB) bütün doğruya (AB)oranına eşit olsun.
Altın Oran, pi (π) gibi irrasyonel bir sayıdır ve ondalık sistemde yazılışı; 1.618033988749894... dür. (noktadan sonraki ilk 15 basamak). Bu oranın kısaca gösterimi olur. Altın Oranın ifade edilmesi için kullanılan sembol, PHI yani Φ'dir.
Altın Oran ın Görüldüğü ve Kullanıldığı Yerler
1. Ayçiçeği: Ayçiçeği nin merkezinden dışarıya doğru sağdan sola ve soldan sağa doğru tane sayılarının birbrine oranı, altın oranı verir.
2. Papatya Çiçeği: Papatya Çiçeğinde de ayçiçeğinde olduğu gibi bir altın oran mevcuttur.
3. Insan Kafası: Bildiğiniz gibi her insanın kafasında bir ya da birden fazla saçların çıktığı düğüm noktası denilen bir nokta vardır. Işte bu noktadan çıkan saçlar doğrusal yani dik değil, bir spiral, bir eğri yaparak çıkmaktadır. Işte bu spiralin ya da eğrinin tanjantı yani eğrilik açısı bize altın oranı verecektir.
4.Kollar: Insan vücudunun bir parçası olan kolları dirsek iki bölüme ayırır(Büyük(üst) bölüm ve küçük(alt) bölüm olarak). Kolumuzun üst bölümünün alt bölüme oranı altın oranı verceği gibi, kolumuzun tamamının üst bölüme oranı yine altın oranı verir.
5.Parmaklarınızın üst boğumunun alt boğuma oranı altın oranı vereceği gibi, parmağınızın tamamının üst boğuma oranı yine altın oranı verir.
6. Mısır Piramitleri: Her bir piramitin tabanının yüksekliğine oranı yine altın oranı veriyor.
7.Mona Lisa: Bu tablonun boyunun enine oranı altın oranı verir.
7.Aziz Jerome: Yine tablonun boyunun enine oranı bize altın oranı verir.
8. Çam Kozalağı: Çam kozalağındaki taneler kozalağın altındaki sabit bir noktadan kozalağın tepesindeki başka bir sabit noktaya doğru spiraller (eğriler) oluşturarak çıkarlar. Işte bu eğrinin eğrilik açısı altın orandır.
9. Deniz Kabuğu: deniz kabuğunun yapısı incelendiğinde bir eğrilik tespit edilmiş ve bu eğriliğin tanjantının altın oran olduğu görülmüştür.
10. Tütün Bitkisi: Tütün Bitkisinin yapraklarının dizilişinde bir eğrilik söz konusudur. Bu eğriliğin tanjantı altın orandır.
11. Eğrelti Otu: Tütün Bitkisindeki aynı özellik Eğrelti Otu nda da vardır.
12. Elektrik Devresi: Altın Oran sadece Matematik ve kainatta değil, Fizik te de kullanılıyor. Verilen n tane dirençten maximum verim elde etmek için bir paralel bağlama yapılması gerekir. Bu durumda Eşdeğer Direnç, yani Reş= yani altın oran olur.
14. Salyangoz: Salyangozun Kabuğu bir düzleme aktarılırsa, bu düzlem bir dikdörtgen oluşturur (-ki biz bu dikdörtgene altın dikdörtgen diyoruz.-) Işte bu dikdörtgenin boyunun enine oranı yine altın oranı verir.
15.Mimar Sinan ın da bir çok eserinde bu altın oran görülmektedir. Mesela Süleymaniye ve Selimiye Camileri nin minarelerinde bu oran görülmektedir.
İNSAN VÜCUDUNDA ALTIN ORAN
Insan gözünün ALTIN ORAN a bu kadar yakın olmasının, estetik açıdan sürekli olarak ALTIN ORAN a uygun şekil ve yapıları tercih etmesinin bir nedenini, yaşadığı çevre olan doğada hemen her an ALTIN ORAN la karşı karşıya olmasının yanı sıra, kendi vücudunun hemen her noktasında ALTIN ORAN a sahip olmasında arayabiliriz. Aşağıda oranlarda insanında ne kadar ALTIN ORAN örneği olduğunu göreceksiniz:
INSAN YÜZÜNDE ALTIN ORAN
Ideal ölçülere sahip bir insan yüzünde de sayısız ALTIN ORAN örnekleri görmek mümkündür:
- Yüz yüksekliği/Yüz genişliği
- Tepe - Göz yüksekliği/Saç Dibi - Göz Yüksekliği
- Göz - çene arası/Burun - çene arası
- Alın genişliği/Burun boynu
- Göz - Ağız/Burun boyu
- Burun altı - çene/Ağız – Çene
- Yüz genişliği/Gözbebekleri arası
- Gözbebekleri arası/Ağız genişliği
- Ağız genişliği/Burun Genişliği
Sakın bunları okuduktan sonra elinize kağıt kalem cetvel alıp yüzünüzü gözünüzü ölçmeye başlamayın.Zira bu sözünü ettiğimiz sayı doğadaki ideal düzeni temsil etmektedir.Eski yunan ve mısır medeniyetlerinde daha sık görülmesinin ve üstünde çalışılmasının en temel sebebi bahsettiğimiz uygarlıkların doğayla uyumundan kaynaklanmatadır.Günümüz dünyasında ne kadar doğadan uzaklaşırsak estetiğin sembolü Altın orandan da uzaklaşmış oluruz...


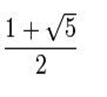












0 yorum:
Yorum Gönder